数式(2.7),p.19,は球対称の場合の拡散方程式です.さらりと書いてありますが.....なかなかくせ者です.
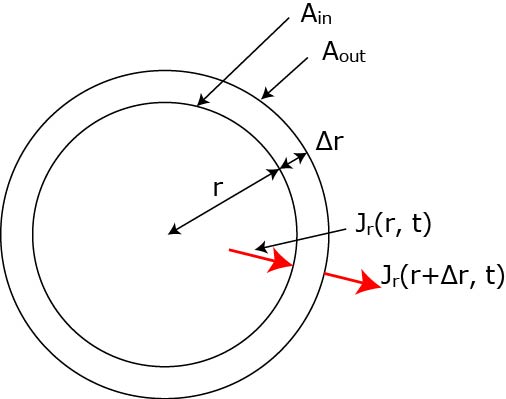
まずは,図2.3に習って球の場合を考えていきましょう.

このように,球殻に入る流れ,出て行く流れを考えると,p.18の式と同様に考え,
\(\Large \frac{1}{\tau} [C (t + \tau) -C (t)] = -\frac{1}{\tau} [J_{r} (r + \Delta r) \cdot A_{out} - J_{r} (r) \cdot A_{in} ] \frac{\tau}{A \cdot \Delta r} \)
ここで,分母のAはin,out,どちらかというと最終的にはΔr→0,としますので,どちらでもいい(計算では,Ain)と思います.球の表面積の公式から,
\(\Large = -\frac{1}{\tau} [J_{r} (r + \Delta r) \cdot 4 \pi (r + \Delta r)^{2}- J_{r} (r) \cdot 4 \pi r^{2} ] \frac{\tau}{4 \pi r^{2} \cdot \Delta r} \)
\(\Large = -\frac{1}{\tau} [J_{r} (r + \Delta r) \cdot (r + \Delta r)^{2}- J_{r} (r) \cdot r^{2} ] \frac{\tau}{ r^{2} \cdot \Delta r} \)
\(\Large = - [J_{r} (r + \Delta r) \cdot \frac{ (r + \Delta r)^{2}}{r^{2} \cdot \Delta r}- J_{r} (r) \cdot \frac{ r^{2}}{r^{2} \cdot \Delta r} ] \)
\(\Large = - [\frac{J_{r} (r + \Delta r) - J_{r} (r)}{ \Delta r}+ \frac{2 J_{r} (r + \Delta r)}{r} + \frac{ J_{r} (r + \Delta r) \cdot \Delta r}{r^2} ] \)
となります.
ここで,Δr→0,とすれば,
\(\Large \frac{\partial C}{\partial{t}} = -\lbrack \frac{\partial J_r}{\partial r} + \frac{2 J_r}{r}\rbrack \)
となります.式(2.6)にありますように,
\(\Large J_r = - D \frac{\partial C}{\partial r} \)
なので,
\(\Large \begin{align*} \frac{\partial C}{\partial{t}} &= D \lbrack \frac{\partial^2 C}{\partial r^2} + \frac{2}{r} \frac{\partial C}{\partial r} \rbrack \\
&= D
\frac{1}{r^2} \frac{\partial}{\partial r} \lbrack r^2 \frac{\partial C}{\partial r} \rbrack \end{align*} \)
とまとめることができ,式(2.7)を導き出すことができました.